Populate right neighbors for all nodes in a binary tree
Given a binary tree with each node having a reference for its 'neighbor' node along with left and right child nodes. A 'neighbor' node for node 'n' is defined as the node located on the immediate right hand side of node 'n'. A node and its neighbor node would be on the same level. If there is no node located on the immediate right hand side of node 'n', then neighbor of node 'n' is null.
Class definition of tree node having reference to neighbor node looks like following in java.
class TreeNode
{
TreeNode left;
TreeNode right;
TreeNode neighbor;
int value;
public TreeNode(int value)
{
this.value = value;
}
}
As illustrated below, original tree on left hand side would be modified to the tree on the right hand side after populating neighbors for all nodes. 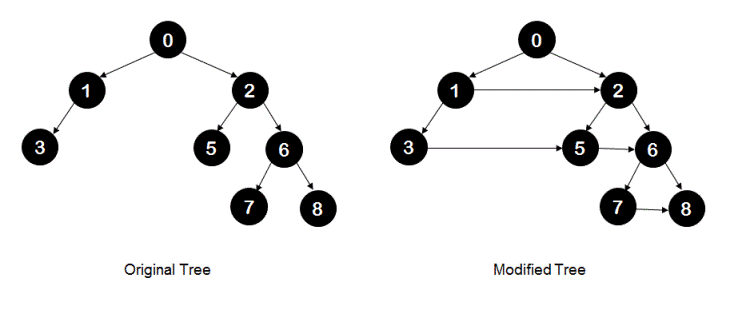
Write a program that populates neighbors for all nodes in a binary tree. This has to be done using recursion and in O(1) explicit extra space.
Please add comments in case you have any queries/feedback.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
This algorithm uses pre-order traversal to populate the right neighbors for all nodes. We will be making use of term 'neighbor' instead of 'right neighbor' in the explanation below for ease of its use.
Since this approach is a top-down approach, it is safe to assume that when we are populating neighbors for child nodes of current node, current node's neighbor is already populated. Using this assumption, it is now easy to populate neighbors for current node's child nodes. While populating neighbors, we are populating neighbors in the right sub-tree before populating neighbors in the left sub-tree. This allows us to access all nodes at the level of current node using neighbor-node chain while populating neighbors for current node's child nodes.
1. First we populate 'neighbor for left child of current node'. If current node's left child is not null then
1a. If 'right child of current node' is not null then we make 'right child of current node' as the neighbor of left child of current node.
1b. If 'right child of current node' is null then we need to find the first non-null node after the left child at left child's level and make that node as left child's neighbor.
Here is the Java code snippet which populates neighbor of current node's left child using steps 1a and 1b.
For example, in the following tree when current node is '1', its neighbor is already populated and we populate neighbor of node '3' here. 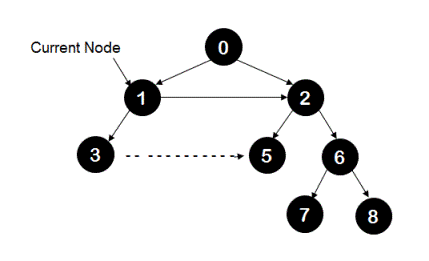
2. To populate the 'neighbor for right child of current node', we use same logic as step #1b. We find the first non-null node after the right child at its level and make that node as the neighbor of right child.
Here is the Java code snippet which implements this step.
3. Once neighbors for current node's child nodes are populated, we make recursive calls to populate neighbors for nodes in left and right sub-trees.
Please checkout function populateNeighbors(TreeNode root) for implementation details. If 'n' denotes total number of nodes in a given binary tree, then the time complexity of this algorithm is O(n). Though the explicit extra space used is O(1), actual space complexity of this algorithm is O(log(n)) since call stack would have O(log(n)) frames in it when neighbors for leaf node are being populated.
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.nilesh.questions;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Uses top down recursion to populate right neighbors for all nodes in a binary tree.
* @author Nilesh
*/
public class PopulateRightNeighbors
{
private class TreeNode
{
TreeNode left;
TreeNode right;
TreeNode neighbor;
int value;
public TreeNode(int value)
{
this.value = value;
}
}
TreeNode root;
/*
0
1 2
3 5 6
7 8
*/
public TreeNode createTree()
{
this.root = new TreeNode(0);
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
TreeNode n7 = new TreeNode(7);
TreeNode n8 = new TreeNode(8);
root.left = n1;
root.right = n2;
n1.left = n3;
n2.left = n5;
n2.right = n6;
n6.left = n7;
n6.right = n8;
return root;
}
private void populateNeighbors(TreeNode root)
{
if (root == null)
{
return;
}
// populate the right neighbor for left child
if (root.left != null)
{
if (root.right != null)
{
root.left.neighbor = root.right;
}
// find first non-null node after left child at its level
else
{
TreeNode parentNeighbor = root.neighbor;
TreeNode neighborNode;
while (parentNeighbor != null)
{
neighborNode = (parentNeighbor.left != null)? parentNeighbor.left : parentNeighbor.right;
// we have found the non-null neighbor for left child
if (neighborNode != null)
{
root.left.neighbor = neighborNode;
break;
}
parentNeighbor = parentNeighbor.neighbor;
}
}
}
// populate the right neighbor for right child
if (root.right != null)
{
// find first non-null node after right child at its level
TreeNode parentNeighbor = root.neighbor;
TreeNode neighborNode;
while (parentNeighbor != null)
{
neighborNode = (parentNeighbor.left != null)? parentNeighbor.left : parentNeighbor.right;
// we have found the non-null neighbor for right child
if (neighborNode != null)
{
root.right.neighbor = neighborNode;
break;
}
parentNeighbor = parentNeighbor.neighbor;
}
}
/*
Populating neighbors in the right sub-tree before that of left sub-tree
allows us to access all nodes at the level of current node using neighbor-node chain
while populating neighbors for current node's child nodes.
*/
// populate neighbors in the right sub-tree first
populateNeighbors(root.right);
// and then populate neighbors in the left sub-tree
populateNeighbors(root.left);
}
private void traverseUsingNeighbors(TreeNode root)
{
TreeNode currentNode = root;
while (currentNode != null)
{
TreeNode temp = currentNode;
currentNode = null;
// print all the nodes in the current level
while(temp != null)
{
// keep checking for the left-most node in the level below the current level
// that is where traversal for next level is going to start
if (currentNode == null)
{
currentNode = (temp.left != null) ? temp.left : temp.right;
}
System.out.print(temp.value + " ");
temp = temp.neighbor;
}
System.out.print("\n\n");
}
}
public void populateNeighbors()
{
populateNeighbors(root);
}
public void traverseUsingNeighbors()
{
traverseUsingNeighbors(root);
}
public static void main(String[] args)
{
PopulateRightNeighbors tree = new PopulateRightNeighbors();
/*
0
1 2
3 5 6
7 8
*/
tree.createTree();
tree.populateNeighbors();
tree.traverseUsingNeighbors();
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(log(n))
