Spiral Level Order Traversal of a Binary Tree | Set 2
Given a binary tree, write a program to traverse the nodes of the given tree in spiral order without using explicit extra space. Your program can simply print the value of node to indicate that it is visited.
Example: For the following tree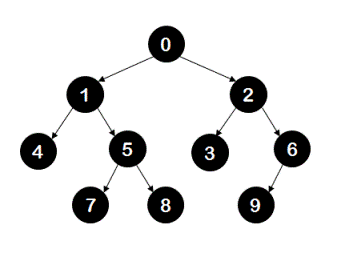
your program's output should be 0,1,2,6,3,5,4,7,8,9.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
In this post, we have explained how a given tree can be traversed in spiral order by making use of stacks and without using recursion. We need to make use of recursion to avoid using explicit extra space.
The recursive algorithm for traversing the given tree in spiral order is also simple. For each level 'i' of the tree(starting from level 0 up to maximum depth of tree), we traverse the tree in pre-order fashion. For a level 'i', instead of traversing the complete tree using pre-order traversal, we just traverse the tree upto level 'i' and when we visit nodes at level 'i', we print them out. Because we need to print the nodes in spiral order, we visit the nodes at level 'i' in left-to-right order when level 'i' is an odd number otherwise we visit nodes in right-to-left order.
You may want to refer to following pictorial representation of spiral order traversal of a tree for more clarity.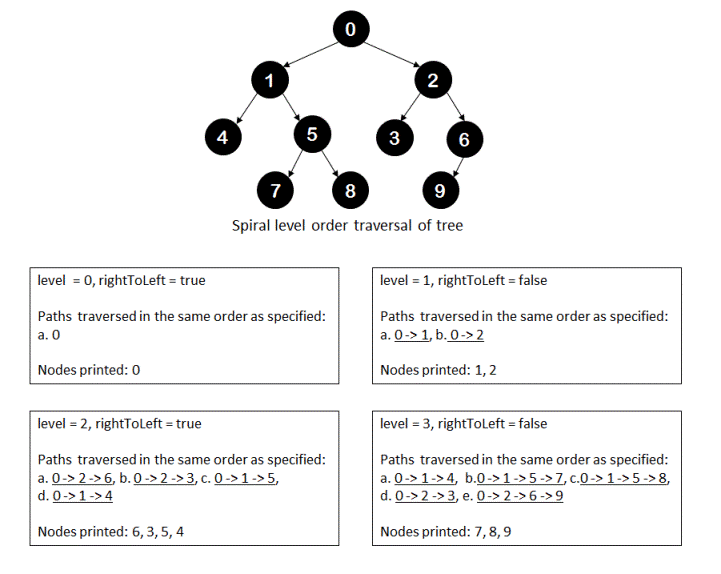
If 'n' is the depth of the tree then the time complexity of this algorithm is O(n^2) since root node which is at level 0 is visited 'n' times, nodes at level 1 are visited 'n-1' times and so on.
The space complexity of this algorithm would be O(n) with 'n' again being the depth of the tree since at any point of time maximum number of stack frames that could be present in memory is 'n'.
You can refer to this post for more details about time and space complexity of recursive algorithms.
Algorithm Visualization
Code Snippet
package com.ideserve.nilesh.questions;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Visits nodes of a binary tree in spiral level order using recursion.
* This algorithm takes O(n^2) time to run where 'n' is the depth of the given tree.
* @author Nilesh
*/
public class SpiralTraversal
{
private class TreeNode
{
TreeNode left;
TreeNode right;
int value;
public TreeNode(int value)
{
this.value = value;
}
}
TreeNode root;
/*
0
1 2
4 5 3 6
7 8 9
*/
public void createTree()
{
this.root = new TreeNode(0);
TreeNode n1 = new TreeNode(1);
TreeNode n2 = new TreeNode(2);
TreeNode n3 = new TreeNode(3);
TreeNode n4 = new TreeNode(4);
TreeNode n5 = new TreeNode(5);
TreeNode n6 = new TreeNode(6);
TreeNode n7 = new TreeNode(7);
TreeNode n8 = new TreeNode(8);
TreeNode n9 = new TreeNode(9);
root.left = n1;
root.right = n2;
n1.left = n4;
n1.right = n5;
n2.left = n3;
n2.right = n6;
n5.left = n7;
n5.right = n8;
n6.left = n9;
}
private int findDepth(TreeNode currentNode)
{
if (currentNode == null)
{
return 0;
}
return (1 + Math.max(findDepth(currentNode.left), findDepth(currentNode.right)));
}
/*
* This sub-routine basically does pre-order traversal for shortened tree.
* Pre-order traversal could be from right-to-left order OR from left-to-right order -
* depending on the value of parameter - 'rightToLeft'.
*
* Tree shortening is done using by considering tree from level of currentNode
* to passed 'level'.
* If passed level is 0, only the currentNode is considered and currentNode's value is printed.
* If passed level is 1, currentNode and its immediate children are considered.
* If passed level is 2, currentNode,its immediate children
* and children of currentNode's children are considered.
*/
private void printNodesAtLevel(TreeNode currentNode, int currentLevel, int maxLevel, boolean rightToLeft)
{
if (currentNode == null)
{
return;
}
// if we have reached the maximum level for this traversal
if (currentLevel == maxLevel)
{
System.out.print(currentNode.value + ", ");
return;
}
if (rightToLeft)
{
printNodesAtLevel(currentNode.right, currentLevel + 1, maxLevel, rightToLeft);
printNodesAtLevel(currentNode.left, currentLevel + 1, maxLevel, rightToLeft);
}
else
{
printNodesAtLevel(currentNode.left, currentLevel + 1, maxLevel, rightToLeft);
printNodesAtLevel(currentNode.right, currentLevel + 1, maxLevel, rightToLeft);
}
}
public void spiralTraversal()
{
int maxDepth = findDepth(root);
// nodes at even level are printed from right to left and
// nodes at odd level are printed from left to right.
boolean rightToLeft = true;
for (int level = 0; level < maxDepth; level++)
{
// print nodes at given level
printNodesAtLevel(root, 0, level, rightToLeft);
rightToLeft = !rightToLeft;
}
}
public static void main(String[] args)
{
SpiralTraversal solution = new SpiralTraversal();
/*
0
1 2
4 5 3 6
7 8 9
*/
solution.createTree();
solution.spiralTraversal();
}
}
Order of the Algorithm
Time Complexity is O(n^2), n: depth of the tree
Space Complexity is O(n)
