Time and Space Complexity of Recursive Algorithms
In this post, we will try to understand how we can correctly compute the time and the space complexity of recursive algorithms. We will be using recursive algorithm for fibonacci sequence as an example throughout this explanation.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Fibonacci Sequence: In the below screenshot, you can see that the function 'fibonacci(int n)' computes n'th number of fibonacci sequence. The fibonacci sequence is 0,1,1,2,3,5,8,13,21,... . As you can observe 0th number of this sequence is 0, 1st number of this sequence is 1 and so on. In general, if f(n) denotes n'th number of fibonacci sequence then f(n) = f(n-1) + f(n-2). For this recurrence relation, f(0) = 0 and f(1) = 1 are terminating conditions.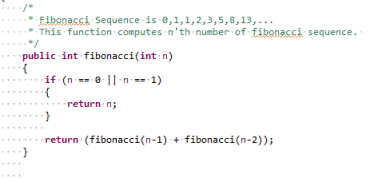
Time Complexity: Let us look at the recursion tree generated to compute the 5th number of fibonacci sequence.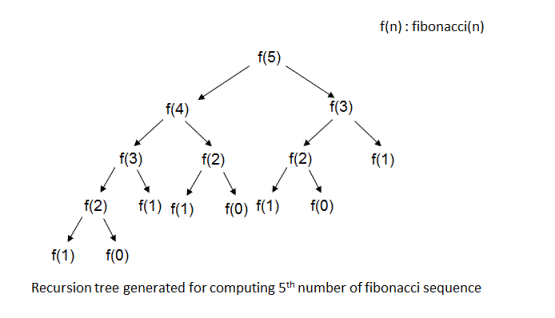
In this recursion tree, each state(except f(0) and f(1)) generates two additional states and total number of states generated are 15. In general, total number of states are approximately equal to 2^n for computing n'th fibonacci number(f(n)). Notice that each state denotes a function call to 'fibonacci()' which does nothing but to make another recursive call. Therefore total time taken to compute nth number of fibonacci sequence is O(2^n).
Note that this does not always hold true and for more accurate time complexity analysis, you should be making use of master theorem. The purpose of this explanation is to give you a general idea about running time of recursive algorithms.
Space Complexity: Computing space complexity of recursive algorithm is little bit tricky. We need to understand how the stack frames are generated in memory for recursive call sequence.
Let's try to understand in general when the stack frames are generated and for how long are they kept in the memory? When a function 'f1' is called from function 'f0', stack frame corresponding to this function 'f1' is created. This stack frame is kept in the memory until call to function 'f1' is not terminated. This stack frame is responsible for saving the parameters of function 'f1', local variables in the function 'f1' and return address of caller function(function 'f0'). Now when this function 'f1' calls another function 'f2', stack frame corresponding to 'f2' is also generated and is kept in the memory until call to 'f2' is not terminated. When call to 'f2' is made, the call stack which has stack frames in it looks like following - 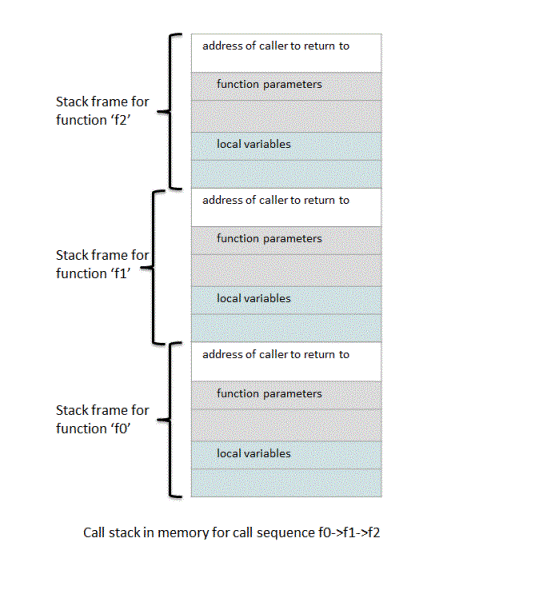
Now when call to function 'f2' returns, the stack frame corresponding to 'f2' is deleted from memory since it is no longer required. Same is the case for stack frames of function 'f1' and function 'f0'.
Using this analogy for recursive call sequence, it should follow that maximum number of stack frames that could be present in memory at any point of time is equal to maximum depth of recursion tree. In the recursion tree, when the call corresponding to leaf node state is getting executed, its call sequence could be represented by the path from the root node in recursion tree to that leaf node. For example, in the recursion tree for computing 5th fibonacci number, when left and bottom most state f(1) is getting executed, the call sequence which led to this state would be f(5)->f(4)->f(3)->f(2)->f(1) and all the corresponding stack frames would be present in the memory and when f(1) is returned its stack frame would be removed from the memory(or call stack).
To conclude, space complexity of recursive algorithm is proportinal to maximum depth of recursion tree generated. If each function call of recursive algorithm takes O(m) space and if the maximum depth of recursion tree is 'n' then space complexity of recursive algorithm would be O(nm).
