Recursive algorithm to solve Towers of Hanoi puzzle
In the problem of the Towers of Hanoi, we are given 3 rods and N disks of different sizes which can slide onto any tower. The initial position of the problem is that the disks are sorted in ascending order of size from top to bottom that is each disk sits on top of an even larger one as shown below. We have to write a program to move the disks from the first rod to the last rod with the following constraints(A move can be simulated by a simple print statement stating the move of the topmost disk of any tower).
(A) Only one disk can be moved at a time.
(B) A disk is slid off the top of one rod onto the next rod.
(C) A disk can only be placed on top of a larger disk.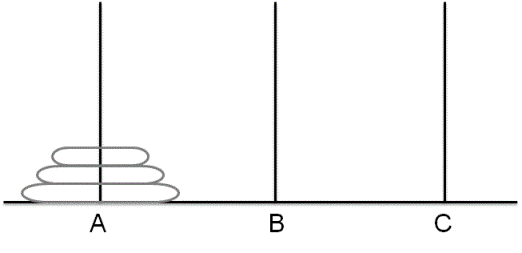
Video coming soon!
Subscribe for more updates
Algorithm/Insights
This is a classic example to understand the intuition of recursion.
Let's first try to understand the abstract procedure that would help to solve this problem.
Without caring too much about the details, from the above given state we first want to reach to the following shown state.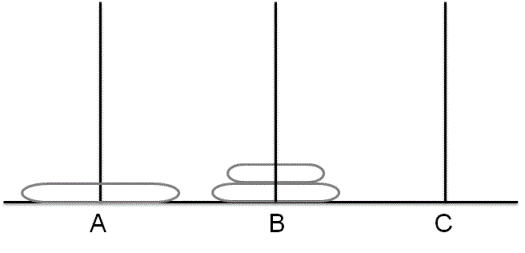
where top two disks are moved to tower 'B' by making use of tower 'C'(if required). Once we get to this state, the last disk in tower A is free to move to tower 'C' and once we move that disk to tower 'C' we reach the following state.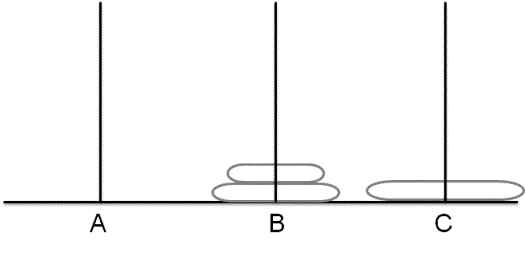
Now from this state, we need to move the two disks sitting at the tower 'B' to tower 'C' using tower 'A'. Once we do that following state is reached and we are done.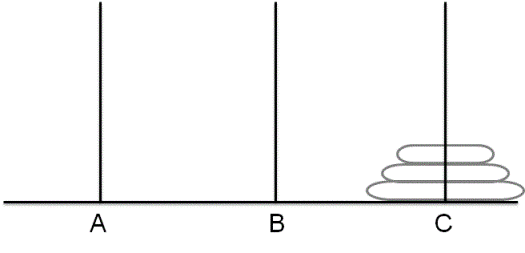
By careful observation of above steps we can formulate the recursive algorithm to solve this problem.
If function 'solve' takes arguments as number of disks to be moved, source tower(A), intermediate tower(B) and destination tower(C) then
1. Initial call is made to function solve(n = n, srcTower = A, intermedTower = B, destTower = C)
2. if (n == 1) then the only disk sitting at srcTower can be moved to destTower. We move that disk to destTower and return to the calling function. This is the base case for this recursion.
for n > 1
3. We want to first move top 'n-1' disks from srcTower to intermedTower using destTower. To do this, we make a recursive call - solve(n = n-1, srcTower = srcTower, intermedTower = destTower, destTower = intermedTower). Note how the roles of intermedTower and destTower have changed for solving this puzzle for 'n-1' disks.
4. After completion of step #3, we make a recursive call solve(n = 1, srcTower = srcTower, intermedTower = intermedTower, destTower = destTower) to move the last disk sitting at srcTower to destTower using intermedTower though intermedTower is not needed in this case. At this step, we are basically hitting the base case for recursion.
5. Lastly, we want to move 'n-1' disks from intermedTower to destTower using srcTower. To do this, we again make a recursive call - solve(n = n-1, srcTower = intermedTower, intermedTower = srcTower, destTower = destTower).Here again, roles of intermedTower and srcTower are exchanged.
Time taken by this algorithm is exponential in nature. As you should be able to verify, to move 'n' disks, minimum number of moves needed are (2^n - 1).
Please checkout code snippet and algorithm visualization section for more details of the algorithm.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Recursion to solve Towers of Hanoi problem.
* @author Nilesh
*/
public class TowerOfHanoiPuzzle {
int steps = 0;
public void solve(int n, String srcTower, String intermediateTower, String destTower)
{
if (n == 1)
{
System.out.println("Move topmost disk from " + srcTower + " to " + destTower);
steps += 1;
return;
}
// first move top n-1 disks to intermediate tower using destination tower
solve(n-1, srcTower, destTower, intermediateTower);
// then move the last disk remaining on source tower to destination tower
solve(1, srcTower, intermediateTower, destTower);
// and finally move n-1 disks which are now in intermediate tower to dest tower using source tower
solve(n-1, intermediateTower, srcTower, destTower);
}
public static void main(String args[])
{
TowerOfHanoiPuzzle problem = new TowerOfHanoiPuzzle();
problem.solve(3, "A", "B", "C");
}
}
Order of the Algorithm
Time Complexity is O(2^n)
Space Complexity is O(1)
