Trie Data Structure | Insert and search
A trie is a data structure used for efficient retrieval of data associated with keys. If key is of length n, then using trie worst case time complexity for searching the record associated with this key is O(n). Insertion of (key, record) pair also takes O(n) time in worst case.
Trie's retrieval/insertion time in worst case is better than hashTable and binary search tree both of which take worst case time of O(n) for retrieval/insertion. The trie structure though in theory has same worst case space complexity as hashTable or a binary tree, memory needed to store pointers causes it to be less space efficient during implementations.
You can see in the below picture as to how a trie data structure looks like for key, value pairs ("abc",1),("xy",2),("xyz",5),("abb",9)("xyzb",8), ("word",5).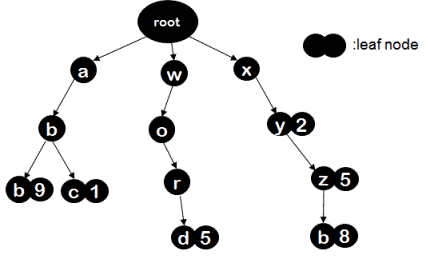
Each node including root has 'n' number of children, where 'n' is total number of possible alphabets out of which a key would be formed. In this example, if we assume that a key would not consist of any other alphabets than characters 'a' to 'z' then value of 'n' would be 26. Each node therefore would point to 26 other nodes. Each node is basically an alphabet in the path from root node to leaf node(which stores value for that key). For example, to search the record associated with key 'abc', we start from root node then go to 0th child since first character in key 'abc' has index of 0 in alphabets. By taking 0th index, we reach node 'a', at this point we go to 1st child and reach node 'b', here we take 2nd path to child and go to node 'c'. Now to reach node 'c', in total we have visited node 'a' then node 'b' followed by node 'c', in other words key 'abc' is visited completely and hence we stop at node 'c' and return the value stored at this node.
We will now go through the precise insertion and search algorithms using the same example.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Construction:
Constructing a trie is equivalent to constructing a root node with following 'TrieNode' definition.
this.root = new TrieNode(false, NON_VALUE); We pass isLeafNode = false, value = NON_VALUE while constructing this root.
class TrieNode
{
boolean isLeafNode;
int value;
TrieNode[] children;
TrieNode(boolean isLeafNode, int value)
{
this.value = value;
this.isLeafNode = isLeafNode;
children = new TrieNode[ALPHABET_SIZE];
}
}
Insertion:
Let's say we want to insert a key-value pair ("abc",1) into the trie.
1. We go to root node.
2. Get the index of the first character ('a') of "abc". That would be 0 in our alphabet system.
3. Go to 0th child of root. Because 0th child is null we first construct a TrieNode to which this 0th child would point. This newly constructed node would be node 'a'. We mark this node as current node.
4. Now we get the index of the second character of "abc". That would be 1 and therefore we go to 1st child of current node(from step #3).
5. Here again, 1st child is null. We create a new TrieNode which would be node 'b'. We mark this node as current node.
6. Now we get the index of the third character of "abc". That would be 2 and therefore we go to 2nd child current node(from step#5).
7. Here again, 2nd child is null. We create a new TrieNode which would be node 'c'. We mark this node as current node.
8. At this step, we are done reading all the characters of the given key. Hence we mark the current node that is node 'c' as leaf node and store value 1 at this leaf node.
Now at this point let's say we want to insert a key-value pair ("abb",9) into the trie.
1. We go to root node.
2. Get the index of the first character of "abb". That would be 0 in our alphabet system.
3. Go to 0th child of root. Now as you can notice, 0th child won't be null since we have constructed node 'a' in the previous insertion sequence. We mark this node 'a' as the current node.
4. Now we get the index of the second character('b') of "abb". That would be 1, we go to 1st child of current node(from step #3).
5. 1st child of current node which is node 'b' is not null. We mark this node 'b' as current node. We now get the index of the last character ('b') of "abb". That index would be 1 and hence we go to 1st child of current node which is null. We create a new TrieNode which would be node 'b'. Current node now points to this newly created node.
6. We are done reading all characters if given key "abb". We mark current node as leaf node and store value 9 in it.
Hopefully, these steps will help to understand the insertion algorithm better.
Search algorithm steps:
Example-1 : searching for non-existing key "ac"
1. Go to root node.
2. Pick the first character of key "ac" which would be 'a'. Find out its index using alphabet system in use.
3. Index returned would be 0, go to 0th child of root which is node 'a'. Mark this node as current node.
4. Pick the second character of key "ac" which would be 'c'. Its index would be 2 and therefore we go to 2nd child of current node.
5. Now at this point, we find out that 2nd child of current node is null. If you notice, from insertion algorithm of a given key, no node in the key-path from the root could be null. If it is null then that implies that this key was never inserted in the trie. And therefore in such cases, we return 'KEY_NOT_FOUND'.
Example-2 : searching for an existing key "abb"
The steps are very similar to example-1. We keep on reading characters of given key and according to indices of characters, travel from root node to node 'b' which is at level-3 (if root is at level-0). At this point we would have read all the characters of the key "abb" and hence we return the value stored at this node.
Please checkout code snippet and algorithm visualization section for more details of the algorithm.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Construct a trie. Do insert and search operations.
* @author Nilesh
*/
public class Trie {
// we are only dealing with keys with chars 'a' to 'z'
final static int ALPHABET_SIZE = 26;
final static int NON_VALUE = -1;
class TrieNode
{
boolean isLeafNode;
int value;
TrieNode[] children;
TrieNode(boolean isLeafNode, int value)
{
this.value = value;
this.isLeafNode = isLeafNode;
children = new TrieNode[ALPHABET_SIZE];
}
public void markAsLeaf(int value)
{
this.isLeafNode = true;
this.value = value;
}
}
TrieNode root;
Trie()
{
this.root = new TrieNode(false, NON_VALUE);
}
private int getIndex(char ch)
{
return ch - 'a';
}
public int search(String key)
{
// null keys are not allowed
if (key == null)
{
return NON_VALUE;
}
TrieNode currentNode = this.root;
int charIndex = 0;
while ((currentNode != null) && (charIndex < key.length()))
{
int childIndex = getIndex(key.charAt(charIndex));
if (childIndex < 0 || childIndex >= ALPHABET_SIZE)
{
return NON_VALUE;
}
currentNode = currentNode.children[childIndex];
charIndex += 1;
}
if (currentNode != null)
{
return currentNode.value;
}
return NON_VALUE;
}
public void insert(String key, int value)
{
// null keys are not allowed
if (key == null) return;
key = key.toLowerCase();
TrieNode currentNode = this.root;
int charIndex = 0;
while (charIndex < key.length())
{
int childIndex = getIndex(key.charAt(charIndex));
if (childIndex < 0 || childIndex >= ALPHABET_SIZE)
{
System.out.println("Invalid Key");
return;
}
if (currentNode.children[childIndex] == null)
{
currentNode.children[childIndex] = new TrieNode(false, NON_VALUE);
}
currentNode = currentNode.children[childIndex];
charIndex += 1;
}
// mark currentNode as leaf
currentNode.markAsLeaf(value);
}
public static void main(String[] args)
{
Trie tr = new Trie();
tr.insert("aab", 3);
int value = tr.search("aab");
System.out.println(value);
}
}
Order of the Algorithm
Time Complexity is O(n) where n is the length if the key
Space Complexity is O(1)
