Trie Data Structure | Delete
In the previous post, we have seen how can we insert and retrieve keys for trie data structure. In this post, we will discuss how to delete keys from trie.
Background: A trie is a data structure used for efficient retrieval of data associated with keys. If key is of length n, then using trie, worst case time complexity for searching the record associated with this key is O(n). Insertion and deletion of (key, record) pair also takes O(n) time in worst case.
You can see in the below picture as to how a trie data structure looks like for key, value pairs ("abc",1),("xy",2),("xyz",5),("abb",9)("xyzb",8), ("word",5).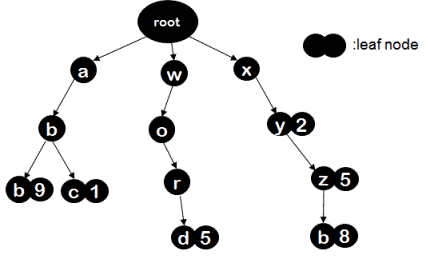
You might want to visit previous post for more details about trie data structure,constructing a trie, insertion and search algorithms, its comparison with other data structures.
Algorithm requirements for deleting key 'k':
1. If key 'k' is not present in trie, then we should not modify trie in any way.
2. If key 'k' is not a prefix nor a suffix of any other key and nodes of key 'k' are not part of any other key then all the nodes starting from root node(excluding root node) to leaf node of key 'k' should be deleted. For example, in the above trie if we were asked to delete key - "word", then nodes 'w','o','r','d' should be deleted.
3. If key 'k' is a prefix of some other key, then leaf node corresponding to key 'k' should be marked as 'not a leaf node'. No node should be deleted in this case. For example, in the above trie if we have to delete key - "xyz", then without deleting any node we have to simply mark node 'z' as 'not a leaf node' and change its value to "NON_VALUE"
4. If key 'k' is a suffix of some other key 'k1', then all nodes of key 'k' which are not part of key 'k1' should be deleted.
For example, in the above trie if we were to delete key - "xyzb", then we should only delete node "b" of key "xyzb" since other nodes of this key are also part of key "xyz".
5. If key 'k' is not a prefix nor a suffix of any other key but some nodes of key 'k' are shared with some other key 'k1', then nodes of key 'k' which are not common to any other key should be deleted and shared nodes should be kept intact. For example, in the above trie if we have to delete key "abc" which shares node 'a', node 'b' with key "abb", then the algorithm should delete only node 'c' of key "abc" and should not delete node 'a' and node 'b'.
We will now go through the algorithm for deleting a record associated with the given key using an example.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The deletion algorithm uses bottom-up recursive algorithm to delete record associated with key 'k'.
The base case for this algorithm is when the node corresponding to last character of key 'k' is reached.
Base Case:
In this algorithm, we keep on passing the level to the child node starting with level 0 for root node. When this level of the node being looked at matches the length of the key, then we know that the node currently being looked at corresponds to last character of key 'k'. In this case, we check if this node has any children. If it has any children then that means this node must be part of other key(s) as well and hence we cannot delete this node. We simply mark this node as a 'non leaf node' and return deletedSelf = false to the parent node(an example of this case would be deletion of key "xyz"). On the other hand, if this node has no children then we know that this node must be the part of only key 'k', therefore we can safely delete this node. We delete the node(by marking currentNode as null) and return deletedSelf = true to the parent node(an example of this case would be deletion of key "word").
If at any point during the key-path traversal we find out that the currentNode is null then we know that this key was never inserted and hence we return deletedSelf = false by printing out the appropriate message('Key Not Found').
Recursion:
When the current node that we are looking at is not the last node for key 'k', then
1. We first make a recursive call to delete the node which is child of the currentNode.
2. We check if child node was deleted in step #1. If child node was not deleted then child node must be shared with some other key which implies this currentNode is also part of some other key and hence we do not delete currentNode and return deletedSelf = false to the parent node.
3. After step #1, if child node was deleted then we check if this currentNode can be deleted. We check that using two conditions: (a) If this node is marked as a leaf node then this node must be the last node corresponding to some other key and hence we return deletedSelf = false without deleting currentNode. (b) If this node has any more children then that means this node is part of some other key as well and hence return deletedSelf = false without deleting currentNode. (c) If both conditions (a) and (b) evaluate to false then we know that this node can be safely deleted. We return deletedSelf = true by marking currentNode as null
Tricky part:
When we make currentNode = null for deleting the current node, current node won't be deleted since we are making only the local reference to the node as null. Note that this node still has got another reference in terms of parent node's child reference. To delete the node completely, what we do is once a child returns deletedSelf as true, we make child reference = null as well. Code for this is code snippet is - if (childDeleted) currentNode.children[getIndex(key.charAt(level))] = null;
Example run through:
Now let's try to understand this algorithm using an example where we delete key "abc" in the trie shown in diagram above.
1. We make a call delete("abc") call which in turn calls deleteHelper(key = "abc", currentNode = root, length = 3, level = 0).
2. In deleteHelper(), we make a recursive call deleteHelper(key = "abc", currentNode = root.children[(getIndex('a'))], length = 3, level = level + 1) to reach node 'a' at level 1.
3. At this step, we again make a recursive call deleteHelper(key = "abc", currentNode = root.children[(getIndex('b'))], length = 3, level = level + 1) to reach node 'b' at level 2.
4. At this step, we again make a recursive call deleteHelper(key = "abc", currentNode = root.children[(getIndex('c'))], length = 3, level = level + 1) to reach node 'c' at level 3.
5. Now at this point level is 3 which is also equal to length. This implies we have reached last node for given key "abc". This is the base case for this algorithm. We check if node 'c' at level 3 has any children. It does not have any children and hence we mark currentNode = null(which refers to node 'c') and return deletedSelf = true.
6. Step #5 returns to call from step #4 where currentNode is 'b'. Since child was deleted we mark currentNode.children[(getIndex('c'))] = null to delete all references to node 'c' at level 3. Then we check if this currentNode 'b' has any more children. It does have one more child 'b' at level 3 (part of "abb") which implies that this node is part of other key and hence we do not delete currentNode and return deletedSelf = false.
7. Step #6 returns to call from step #3. Here currentNode is 'a'. Since child is not deleted, this currentNode also cannot be deleted and we simply return with deletedSelf = false.
8. Same return sequence is repeated until the recursion ends by a return call to function which had curreneNode as root.
At the end of this call sequence, node 'c' at level-3 would have been deleted.
Hopefully, this example will help to understand the algorithm more clearly.
Please checkout code snippet and algorithm visualization section for more details of the algorithm.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Construct a trie. Do insert, search and delete operations.
* @author Nilesh
*/
public class Trie {
// we are only dealing with keys with chars 'a' to 'z'
final static int ALPHABET_SIZE = 26;
final static int NON_VALUE = -1;
class TrieNode
{
boolean isLeafNode;
int value;
TrieNode[] children;
TrieNode(boolean isLeafNode, int value)
{
this.value = value;
this.isLeafNode = isLeafNode;
children = new TrieNode[ALPHABET_SIZE];
}
public void markAsLeaf(int value)
{
this.isLeafNode = true;
this.value = value;
}
public void unMarkAsLeaf()
{
this.isLeafNode = false;
this.value = NON_VALUE;
}
}
TrieNode root;
Trie()
{
this.root = new TrieNode(false, NON_VALUE);
}
private int getIndex(char ch)
{
return ch - 'a';
}
public int search(String key)
{
// null keys are not allowed
if (key == null)
{
return NON_VALUE;
}
TrieNode currentNode = this.root;
int charIndex = 0;
while ((currentNode != null) && (charIndex < key.length()))
{
int childIndex = getIndex(key.charAt(charIndex));
if (childIndex < 0 || childIndex >= ALPHABET_SIZE)
{
return NON_VALUE;
}
currentNode = currentNode.children[childIndex];
charIndex += 1;
}
if (currentNode != null)
{
return currentNode.value;
}
return NON_VALUE;
}
public void insert(String key, int value)
{
// null keys are not allowed
if (key == null) return;
key = key.toLowerCase();
TrieNode currentNode = this.root;
int charIndex = 0;
while (charIndex < key.length())
{
int childIndex = getIndex(key.charAt(charIndex));
if (childIndex < 0 || childIndex >= ALPHABET_SIZE)
{
System.out.println("Invalid Key");
return;
}
if (currentNode.children[childIndex] == null)
{
currentNode.children[childIndex] = new TrieNode(false, NON_VALUE);
}
currentNode = currentNode.children[childIndex];
charIndex += 1;
}
// mark currentNode as leaf
currentNode.markAsLeaf(value);
}
private boolean hasNoChildren(TrieNode currentNode)
{
for (int i = 0; i < currentNode.children.length; i++)
{
if ((currentNode.children[i]) != null)
return false;
}
return true;
}
private boolean deleteHelper(String key, TrieNode currentNode, int length, int level)
{
boolean deletedSelf = false;
if (currentNode == null)
{
System.out.println("Key does not exist");
return deletedSelf;
}
// base case: if we have reached at the node which points to the alphabet at the end of the key.
if (level == length)
{
// if there are no nodes ahead of this node in this path
// then we can delete this node
if (hasNoChildren(currentNode))
{
currentNode = null;
deletedSelf = true;
}
// if there are nodes ahead of this node in this path
// then we cannot delete this node. We simply unmark this as leaf
else
{
currentNode.unMarkAsLeaf();
deletedSelf = false;
}
}
else
{
TrieNode childNode = currentNode.children[getIndex(key.charAt(level))];
boolean childDeleted = deleteHelper(key, childNode, length, level + 1);
if (childDeleted)
{
// tricky
// making children pointer also null: since child is deleted
currentNode.children[getIndex(key.charAt(level))] = null;
// if this is leaf node that means this is part of another key
// and hence we can not delete this node and it's parent path nodes
if (currentNode.isLeafNode)
{
deletedSelf = false;
}
// if childNode is deleted but if this node has more children then this node must be part of another key.
// we cannot delete this node
else if (!hasNoChildren(currentNode))
{
deletedSelf = false;
}
// else safely delete this node
else
{
currentNode = null;
deletedSelf = true;
}
}
else
{
deletedSelf = false;
}
}
return deletedSelf;
}
public void delete(String key)
{
if ((root == null) || (key == null))
{
System.out.println("Null key or Empty trie error");
return;
}
deleteHelper(key, root, key.length(), 0);
return;
}
public static void main(String[] args)
{
Trie tr = new Trie();
// tr.insert("word", 5);
tr.insert("xyz", 5);
tr.insert("xyzb", 8);
tr.insert("abb", 9);
tr.insert("abc", 1);
tr.delete("abc");
System.out.println("Deleted key \"abc\"");
String key = "abb";
int value = tr.search(key);
if (value != NON_VALUE)
{
System.out.println("Key-value pair retrieved");
System.out.println("for key \"" + key + "\" value is " + value);
}
}
}
Order of the Algorithm
Time Complexity is O(n) where n is the length if the key
Space Complexity is O(1)
