Pancake Sorting
Given an array of integers, sort the array using a given Flip operation.
This is called Pancake sorting because this uses Flip operation which is analogous to flipping pancakes.
For example, if there are 5 pancakes stacked one of top of the other, then Flip operation is when a spatula is inserted at any point in the stack and then turned upside down flipping all pancakes above it.
Flip operation is defined on the array as:
flip(array, end) = reverse the array elements from 0 to end (inclusive)
Example:
Consider the array:
array[] = {4,1,2,5,3}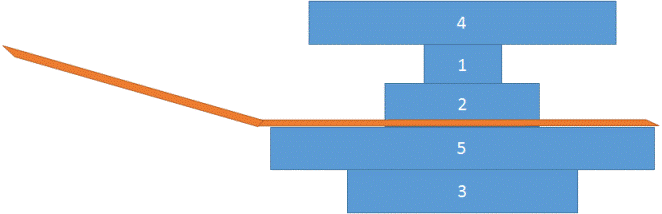
flip(array, 2) will change the array to {2,1,4,5,3}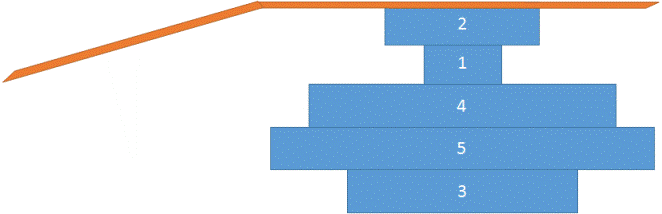
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The problem can be solved by using a modified version of Selection Sort algorithm.
The solution is to find the maximum element and move it to the end of the array using the flip operation. Next find 2nd maximum element and move it is 2nd last position and so on.
For i = n-1 to 1 (where n is length of the array) do following steps:
1. Find the index of the maximum element in the array.
2. Flip array[0..maxIdx] to move ith max element to first position
3. Flip array[0..i] to move ith max element to ith position
Example:
4 1 2 5 3
i = n-1 = 4
MaxIndex from 0 to i is 3 (index of 5)
Flip array[0..3]: (sub array within square brackets [] represents the flipped array)
[5 2 1 4] 3
Flip array[0..i]:
[3 4 1 2 5]
Note that now 5 has been moved to its final position.
3 4 1 2 5
i = 3
MaxIndex from 0 to i is 1 (index of 4)
Flip array[0..1]:
[4 3] 1 2 5
Flip array[0..i]:
[2 1 3 4] 5
Note that now 4 has been moved to its final position.
2 1 3 4 5
i = 2
MaxIndex from 0 to i is 2 (index of 3)
MaxIndex == i, so 3 is already at its correct position.
2 1 3 4 5
i = 1
MaxIndex from 0 to i is 0 (index of 2)
MaxIndex = 0, so no need to call Flip array[0..maxIndex] because our aim is to get (n-i)th maximum number to 0th index. Since its already in 0th index, so no need to call Flip array[0..maxIndex]
Flip array[0..i]:
[1 2] 3 4 5
Note that now 2 has been moved to its final position.
1 2 3 4 5
Hence we get the sorted array:
1 2 3 4 5
Algorithm Visualization
Code Snippet
package com.ideserve.questions.saurabh;
import java.util.Arrays;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Given an array, sort the array using Pancake sort.
*
* @author Saurabh
*
*/
public class PancakeSort {
public static void pancakeSort(int[] array) {
int n = array.length;
for(int i = n-1; i > 0; i--) {
int maxIdx = getMaxValueIndex(array, i); // Find (n-i)th max element
if(maxIdx != i) {
if(maxIdx != 0) {
flip(array, maxIdx); // Flip array[0...maxIdx] to move ith max element to first position
}
flip(array, i); // Flip array[0...i-1] to move ith max element to ith position
}
}
}
// Flip operation
private static void flip(int[] array, int end) {
int start = 0;
while(start < end) {
swap(array, start, end);
start++;
end--;
}
}
private static void swap(int[] array, int start, int end) {
int tmp = array[start];
array[start] = array[end];
array[end] = tmp;
}
private static int getMaxValueIndex(int[] array, int end) {
int max = 0;
for(int i = 1; i <= end; i++) {
if(array[max] < array[i]) {
max = i;
}
}
return max;
}
public static void main(String[] args) {
int[] array = {4,1,2,5,3};
pancakeSort(array);
System.out.println(Arrays.toString(array));
}
}
Order of the Algorithm
Time Complexity is O(n^2). The algorithm invokes getMaxValueIndex (n-1) and flip operation 2*(n-1) times in the worst case. getMaxValueIndex has O(n) time complexity and flip operation has complexity O(n).
Space Complexity is O(1)
