Remove the nodes of binary search tree which are outside the given range
Given a binary search tree(BST) and a range of numbers ['min' to 'max'], remove all nodes of a given BST which are not in the given range. Any node having value less than 'min' or having value greater than 'max' should be removed. The condition is that after removing the nodes, modified BST should be still a BST.
For example, in the below BST all the nodes which are out of the range [3,9] are removed and modified BST is shown on the right hand side.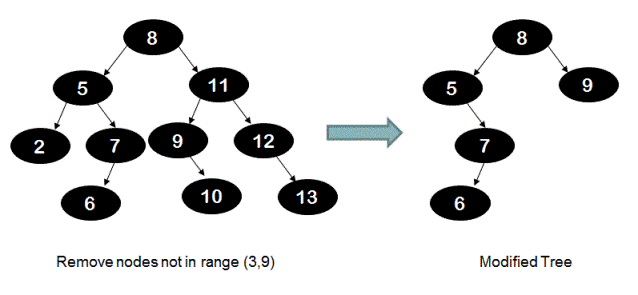
Video coming soon!
Subscribe for more updates
Algorithm/Insights
Generally when there is deletion of nodes involved in a binary tree, post-order traversal is used. Going by the same rule here, we delete the nodes which are outside the given range using post-order traversal. That logically means that by the time value of a node is checked against the given range, it's left and right sub-trees are already in correct states.
In this algorithm, after correcting left and right sub-trees of current node using recursive calls, we check the value of currentNode itself to see if it is in the given range['min' - 'max']. If it is in the correct range we return the reference of currentNode without doing anything. If we find that value of currentNode is less than 'min' limit then we need to simply return the reference of right child of currentNode to the calling function. This is because in this case all nodes in currentNode's left sub-tree would have had value less than min and therefore they would have already been deleted(remember we are using post-order traversal). Also the nodes in the right sub-tree of currentNode which would have had value less than 'min' would have been deleted and right sub-tree for currentNode now is in correct state. In very similar manner, if the value of currentNode is greater than the 'max' limit of specified range then we need to simply return the reference of left child of currentNode to the calling function.
Below tree diagram illustrates what value is returned at each node with this algorithm. Note that node '11' returns reference to node '9' and not null.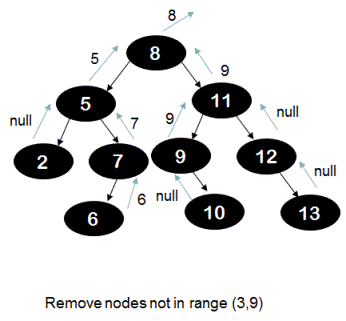
The time complexity of this algorithm is O(n) with O(n) auxiliary space usage. You may want to check out this post which explains time and space complexity of recursive algorithms in general.
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.LinkedList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Removes nodes of a given BST which are out of given range [n1 - n2]
* @author Nilesh
*/
public class RemoveOutOfRangeNodesBST
{
private class QueueNode
{
BinarySearchTreeNode treeNode;
int level;
QueueNode(BinarySearchTreeNode treeNode, int level)
{
this.treeNode = treeNode;
this.level = level;
}
}
private class BinarySearchTreeNode
{
int data;
BinarySearchTreeNode left;
BinarySearchTreeNode right;
BinarySearchTreeNode(int data)
{
this.data = data;
}
}
BinarySearchTreeNode root;
RemoveOutOfRangeNodesBST()
{
}
private BinarySearchTreeNode insert(BinarySearchTreeNode node, int key)
{
if (node == null) // base case
{
node = new BinarySearchTreeNode(key);
}
if (key < node.data) // insert key into left sub-tree
{
node.left = insert(node.left, key);
}
else if (key > node.data) // insert key into right sub-tree
{
node.right = insert(node.right, key);
}
return node;
}
public void insert(int key)
{
root = insert(this.root, key);
return;
}
public void printTreeLevelOrder()
{
if (root == null) return;
LinkedList queue = new LinkedList();
queue.add(new QueueNode(root, 0));
int maxLevelVisited = -1;
while (!queue.isEmpty())
{
QueueNode currentNode = (QueueNode) queue.remove();
if (currentNode.level > maxLevelVisited)
{
maxLevelVisited = currentNode.level;
System.out.print("\nlevel-" + currentNode.level + " nodes: ");
}
System.out.print(" " + currentNode.treeNode.data);
if (currentNode.treeNode.left != null)
{
queue.add(new QueueNode(currentNode.treeNode.left, currentNode.level + 1));
}
if (currentNode.treeNode.right != null)
{
queue.add(new QueueNode(currentNode.treeNode.right, currentNode.level + 1));
}
}
}
private BinarySearchTreeNode removeOutOfRangeNodes(BinarySearchTreeNode currentNode, int min, int max)
{
if (currentNode == null)
{
return null;
}
// correct left and right sub-trees first
currentNode.left = removeOutOfRangeNodes(currentNode.left, min, max);
currentNode.right = removeOutOfRangeNodes(currentNode.right, min, max);
/*
* if currentNode's value is less than min threshold, it's left sub-tree would already be null
* simply return reference to right sub-tree
*/
if (currentNode.data < min)
{
return currentNode.right;
}
/*
* if currentNode's value is more than max threshold, it's right sub-tree would already be null
* simply return reference to left sub-tree
*/
if (currentNode.data > max)
{
return currentNode.left;
}
return currentNode;
}
public void removeOutOfRangeNodes(int min, int max)
{
this.root = removeOutOfRangeNodes(this.root, min, max);
}
public static void main(String[] args)
{
RemoveOutOfRangeNodesBST tree = new RemoveOutOfRangeNodesBST();
tree.insert(8);
tree.insert(5);
tree.insert(11);
tree.insert(2);
tree.insert(7);
tree.insert(9);
tree.insert(12);
tree.insert(6);
tree.insert(10);
tree.insert(13);
/*
* 8
* 5 11
* 2 7 9 12
* 6 10 13
*/
tree.printTreeLevelOrder();
tree.removeOutOfRangeNodes(3, 9);
System.out.print("\n\nBST after removing relevant nodes");
/*
* 8
* 5 9
* 7
* 6
*/
tree.printTreeLevelOrder();
}
}
Order of the Algorithm
Time Complexity is O(n)
Space Complexity is O(n)
