Pattern matching using Trie
Given a pattern and text, find all the occurrences of pattern in given text. For example, in given text "banana" pattern "ana" occurs twice - starting at index 1 and starting at index 2.
Reference used for the example: https://www.biostat.wisc.edu/bmi776/lectures/suffix-trees.pdf
Video coming soon!
Subscribe for more updates
Algorithm/Insights
This algorithm uses trie data structure for time efficient pattern matching for a given pattern in given text. You might want to visit previous posts for more details about trie data structure,constructing a trie, insertion and search algorithms, its comparison with other data structures. In the previous posts, we have also discussed KMP algorithm for pattern matching.
The first step of this algorithm is to construct a trie from given text. To construct this trie, all the suffixes of text are inserted into the trie. For example, if given text is "banana" then all suffixes that is "banana","anana","nana","ana","na","a" are inserted. The trie looks like below image after inserting these suffixes.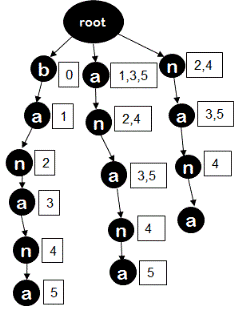
At the time of insertion, each node also stores the indices where the character corresponding to that node occurs in the text and that character is the last character of the sub-string starting from root node. Let's call these indices magic-indices. For example, node 'b' stores index 0 since it occurs at index 0 in text "banana" for sub-string "b". Similarly, node 'a' at level-3 (in the path "root->a->n->a") stores indices 3,5 because letter 'a' is at index 3 and at index 5 in text "banana" and is the last character for sub-string "ana". Similarly, node 'n' at level-3 (path "root->n->a->n") stores index 4 because for substring "nan" it is the last character and it occurs at index 4 in text "banana". We will go through the modified insertion algorithm to understand how this can be easily done. But before that, we will go through the algorithm that uses this modified trie.
Once we have this modified trie in place, all we need to is to traverse the trie by taking out characters of the given pattern one by one and at the end of traversal, return the indices( with appropriate modifications) stored at node reached at the end of the traversal. If during this traversal, we reach the null node then we print out the message that this pattern does not exist in the text and return.
For example, to search for pattern "ana", we will start traversing the trie from root node and we will reach node 'a' at level-3 at the end of the traversal by taking path "root->a->n->a". The indices stored at this node 'a' are 3 and 5. We return these indices by subtracting (pattern length - 1) from each of these. Returned indices would then indicate the start index in the text for the pattern that we are searching for("ana"). For this example, returned indices would be 1 and 4 and as you can verify pattern "ana" is there in text "banana" starting at index 1 and at index 4.
Now let's look at the modified trie insertion algorithm which inserts suffixes of text in tree. This insertion algorithm takes an extra argument along with the key itself. The extra argument is the index in the text where this suffix starts from. Let's call this extra argument an offset for suffix. For example, suffix "anana" in "banana" would have an offset of 1 because it starts at index 1, which is passed to insert function along with suffix "anana". Now to add correct magic index at each node, all we need to do is to add this offset of suffix to the index of the character(corresponding to the node) in the suffix and store the result as a magic index at the node. In this example, while inserting suffix "anana", first node 'a' at level-1 stores the index 1 (offset=1, index=0). Then while inserting suffix "ana", the same first node 'a' at level-1 stores the index 3 (offset=3, index=0) and lastly while inserting suffix "a", it stores index 5(offset=3, index=0).
The time taken by this algorithm is O(n^2) where 'n' is the length of the text. This time is essentially taken to build the trie. Note that this is one time activity and subsequent searches of another pattern in this text would take O(m) time where m is the length of the pattern.
The worst case space complexity of this algorithm is O(n^2) where 'n' is the length of the text. This worst case occurs for text like "aaaaa".
Please checkout code snippet for more details of the algorithm.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.ArrayList;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Pattern matching using Trie data structure.
* @author Nilesh
*/
public class TrieForPatternMatching {
// we are only dealing with keys with chars 'a' to 'z'
final static int ALPHABET_SIZE = 26;
final static int NON_VALUE = -1;
class TrieNode
{
ArrayList<Integer> endingIndices;
TrieNode[] children;
TrieNode(boolean isLeafNode, int value)
{
children = new TrieNode[ALPHABET_SIZE];
this.endingIndices = new ArrayList();
}
}
TrieNode root;
TrieForPatternMatching()
{
this.root = new TrieNode(false, NON_VALUE);
}
private int getIndex(char ch)
{
return ch - 'a';
}
public void insert(String key, int offset)
{
// null keys are not allowed
if (key == null) return;
key = key.toLowerCase();
TrieNode currentNode = this.root;
int charIndex = 0;
while (charIndex < key.length())
{
int childIndex = getIndex(key.charAt(charIndex));
if (childIndex < 0 || childIndex >= ALPHABET_SIZE)
{
System.out.println("Invalid Key");
return;
}
if (currentNode.children[childIndex] == null)
{
currentNode.children[childIndex] = new TrieNode(false, NON_VALUE);
}
currentNode = currentNode.children[childIndex];
// add index for this alphabet where it ends in the string
currentNode.endingIndices.add(charIndex + offset);
charIndex += 1;
}
}
private void matchAndPrintPattern(String str)
{
if (str == null) return;
TrieNode currentNode = root;
int charIndex = 0;
while ((charIndex < str.length()))
{
if (currentNode == null) break;
currentNode = currentNode.children[getIndex(str.charAt(charIndex))];
charIndex += 1;
}
if (charIndex < str.length())
{
System.out.println("Pattern does not exist.");
}
else
{
System.out.println("Pattern found in text starting at following indices..");
for (int i = 0; i < currentNode.endingIndices.size(); i++)
{
System.out.print(currentNode.endingIndices.get(i) - (str.length() - 1));
System.out.print(",");
}
}
return;
}
private void generateAndInsertSuffixes(String text)
{
for (int i = 0; i < text.length(); i++)
{
this.insert(text.substring(i), i);
}
}
public void printPatternMatches(String text, String pattern)
{
generateAndInsertSuffixes(text);
matchAndPrintPattern(pattern);
}
public static void main(String[] args)
{
TrieForPatternMatching tr = new TrieForPatternMatching();
String text = "banana";
String pattern = "ana";
tr.printPatternMatches(text, pattern);
}
}
Order of the Algorithm
Time Complexity is O(n^2) where 'n' is the length of the text.
Space Complexity is O(n^2) where 'n' is the length of the text.
