Minimum number of trials to reach from source word to destination word
Given a dictionary of words, find minimum number of trials to reach from source word to destination word. A valid trial on word 'w' is defined as either insert, delete or substitute operation of a single character in word 'w' which results in a word 'w1' which is also present in the given dictionary. For example, for dictionary {"BCCI","AICC","ICC","CCI","MCC","MCA", "ACC"}, minimum number of trials to reach from word "AICC" to "ICC" is 1. Only 1 opeartion of deleting character 'A' is required to reach from word "AICC" to word "ICC". Minimum number of trials to reach from "AICC" to "MCC" is 2(AICC->ICC->MCC) and minimum number of trials to reach from "AICC" to "MCA" is 3(AICC->ICC->MCC->MCA).
Now if you notice, there are no valid trials with source as "AICC" and destination as "BCCI" for above dictionary. Hence the output returned by program should be '-1' indicating destination word cannot be reached from source word.
Video coming soon!
Subscribe for more updates
Algorithm/Insights
The valid trial on a word is nothing but an edit operation consisting of either edit or delete or insert operation which results in another word present in given dictionary of words.
Using this definition of valid trial, we can re-model this problem as a graph problem where nodes are created for representing all words in dictionary. If edit distance between two words 'word0' and 'word1' is 1, then an edge is added with cost as 1 between nodes 'n0' and 'n1' representing words 'word0' and 'word1' respectively.
Now to find out the minimum number of trials to reach from 'source' word to 'destination' word, all we need to do is to find out the minimum distance between node representing 'source' word and node representing 'destination' word. Because in this graph, all edges have equal cost of 1, doing a breadth first search or depth first search for 'destination' node starting from 'source' node is sufficient to compute minimum distance between 'source' node and 'destination' node. This minimum distance obtained is nothing but the number of trials required to reach 'destination' word from 'source' word.
Example: If we are asked to find out the minimum number of trials to reach from word "AICC" to word "MCA" for dictionary {"BCCI","AICC","ICC","CCI","MCC","MCA", "ACC"}, then we first create a graph with edges between those nodes which have edit distance of 1 between them. The graph created would look like following - 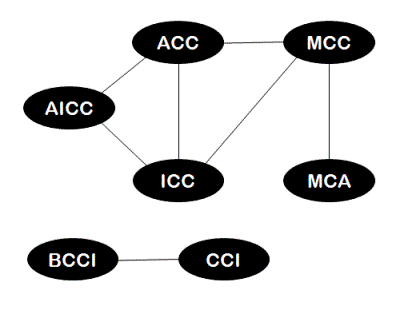
Please note that this graph has two connected components where every node in a component is reachable from every other node. The edges in this graph are bi-directional and hence no direction arrows are shown.
To find out the minimum number of trials to reach from "AICC" to "MCA", we simply start breadth first search from node "AICC" in above graph until we reach node "MCA". While doing breadth first search, starting node "AICC" is assumed to be at level-0, all its neighbors then would be at level-1, neighbors of immediate neighbor of "AICC" would be at level-2 and so on. While doing breadth first search, we keep track of the level of each node visited. During breadth first search, at level-0 only node "AICC" would be visited. At level-1, nodes "ACC" and "ICC" would be visited. Node "MCC" would be visited at level-2 and finally when node "MCA" is visited at level-3, its level that is level-3 is returned since this level would be equal to the minimum number of trials required to reach node "MCA" from node "AICC".
The time complexity of this algorithm is O(m^2.n^2) where 'm' is total number of words in given dictionary and 'n' is the average length of each word. This is because while constructing graph, there are O(m^2) pairs of words for which edit distance is calculated in O(n^2) time. Note that time taken for breadth first search is O(|E|) = O(m^2) in the worst case which is less than time taken for graph building and hence this time is ignored while computing overall time complexity.
Please add comments below in case you have any feedback/queries.
Algorithm Visualization
Code Snippet
package com.ideserve.questions.nilesh;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Iterator;
/**
* <b>IDeserve <br>
* <a href="https://www.youtube.com/c/IDeserve">https://www.youtube.com/c/IDeserve</a>
* Uses graph and minimum edit distance algorithm:
* to find out minimum number of trials to reach from source word to destination word
* @author Nilesh
*/
public class MinimumTrialsSourceToDestWord<T>
{
// used for breadth first search
private class QueueNode
{
GraphNode graphNode;
int level;
// this constructor is used while doing breadth first traversal
public QueueNode(GraphNode node, int level)
{
this.graphNode = node;
this.level = level;
}
}
private class GraphNode
{
T nodeId;
GraphNode next;
int parentDist;
GraphNode(T id)
{
nodeId = id;
next = null;
}
GraphNode(T id, int dist)
{
nodeId = id;
next = null;
parentDist = dist;
}
}
HashMap<T, GraphNode> nodeList;
// create an empty nodelist for holding nodes of graph
public MinimumTrialsSourceToDestWord()
{
nodeList = new HashMap<T, GraphNode>();
}
private void addNode(T id)
{
GraphNode node = new GraphNode(id);
nodeList.put(id, node);
}
private void addEdge(T id1, T id2, int dist)
{
GraphNode node1 = nodeList.get(id1);
if (node1 == null)
{
return;
}
GraphNode node2 = new GraphNode(id2, dist);
node2.next = node1.next;
node1.next = node2;
}
// find the node with required nodeId in graph's node list.
private GraphNode findGraphNode(T nodeId)
{
return nodeList.get(nodeId);
}
// prints adjacency list representation of the graph
public void printGraph()
{
Iterator<T> nodeIterator = nodeList.keySet().iterator();
while (nodeIterator.hasNext())
{
GraphNode curr = nodeList.get(nodeIterator.next());
while (curr != null)
{
System.out.print(curr.nodeId+"("+curr.parentDist+")"+"->");
curr = curr.next;
}
System.out.print("Null");
System.out.println();
}
}
private static int min(int a, int b)
{
return (a<b)?a:b;
}
private static int min(int a, int b, int c)
{
return min(min(a,b),c);
}
// find minimum edit distance between str1 and str2
private static int editDistance(String str1, String str2)
{
// if either of the strings is null, distance cannot be computed
if (str1 == null || str2 == null)
{
return -1; // indicates error input
}
// all values are by default initialized to 0 by JVM
int[][] distanceTable = new int[str1.length()+1][str2.length()+1];
int numRows = str1.length() + 1;
int numCols = str2.length() + 1;
for (int m = 0; m < numRows; m++)
{
for (int n = 0; n < numCols; n++)
{
// if length of str1 is 0, we have no option but to insert all of str2
if (m == 0)
{
distanceTable[m][n] = n;
}
// if length of str2 is 0, delete all of str1 of make it match with str2
else if (n == 0)
{
distanceTable[m][n] = m;
}
/*
* if last characters of str1 and str2 are equal, compute distance ending at
* second last characters for both str1 and str2
*/
else if (str1.charAt(m-1) == str2.charAt(n-1))
{
distanceTable[m][n] = distanceTable[m-1][n-1];
}
/*
* else use minimum of following three cases:
* delete last character of str1 and check distance: distance(str1, str2, m-1, n)
* insert last character of str2 into str1 and check distance: distance(str1, str2, m, n-1)
* replace last char of str1 with last char of str2 and check distance: distance(str1, str2, m-1, n-1)
*/
else
{
distanceTable[m][n] = min (
1 + distanceTable[m-1][n],
1 + distanceTable[m][n-1],
1 + distanceTable[m-1][n-1]
);
}
}
}
return distanceTable[numRows-1][numCols-1];
}
/*
* Does a breadth first traversal of a given graph starting from node with id = srcId.
*/
public int breadthFirstSearch(T srcId, T destId)
{
if (nodeList.isEmpty())
{
System.out.println("Empty graph");
return -1;
}
// queue used during the traversal
LinkedList<QueueNode> queue = new LinkedList();
// keeps track of node which are visited and added into the queue
HashMap<T, Integer> visited = new HashMap();
// find srcNode with id = srcId in graph
GraphNode srcNode = nodeList.get(srcId);
// if srcNode is not there in graph, breadth first traversal which starts at srcNode cannot be done
if (srcNode == null)
{
System.out.println("Source vertex not found");
return -1;
}
int minNumberTrials = -1;
// add srcNode in queue, mark it as visited
queue.add(new QueueNode(srcNode, 0));
visited.put(srcNode.nodeId, 1);
while (!queue.isEmpty())
{
QueueNode currentNode = queue.remove();
// if destination node found
if (currentNode.graphNode.nodeId == destId)
{
minNumberTrials = currentNode.level;
break;
}
// first neighbor of current graph node
GraphNode neighbor = currentNode.graphNode.next;
// add all neighbors of current graph node into the queue
while (neighbor != null)
{
// if this neighbor is not visited earlier, mark it as visited
// add it to the queue at appropriate level
if (visited.get(neighbor.nodeId) == null)
{
visited.put(neighbor.nodeId, 1);
queue.add(new QueueNode(findGraphNode(neighbor.nodeId), currentNode.level + 1));
}
neighbor = neighbor.next;
}
}
return minNumberTrials;
}
// add edges for those strings which have edit distance of 1.
public static void createGraph(MinimumTrialsSourceToDestWord graph, String[] dictionary)
{
// creates nodes: one for each string in the list
for (int i = 0; i < dictionary.length; i++)
{
graph.addNode(dictionary[i]);
}
// add edges only between the nodes which have distance of 1 between them
for (int i = 0; i < dictionary.length; i++)
{
for (int j = 0; j < dictionary.length; j++)
{
if (editDistance(dictionary[i], dictionary[j]) == 1)
{
graph.addEdge(dictionary[i], dictionary[j], 1);
}
}
}
}
public static void main(String[] args)
{
MinimumTrialsSourceToDestWord<String> solution = new MinimumTrialsSourceToDestWord();
String[] dictionary = {"BCCI","AICC","ICC","CCI","MCC","MCA", "ACC"};
createGraph(solution, dictionary);
// prints adjacency list representation of this graph.
// solution.printGraph();
String srcNodeId = "AICC", destNodeId = "MCA";
System.out.print("Minimum number of trials to reach from source word to destination word:\n");
// search destination node from source node using breadth first search
System.out.print(solution.breadthFirstSearch(srcNodeId, destNodeId));
}
}
Order of the Algorithm
Time Complexity is O(m^2.n^2) where m is number of words and n is the average length of word
Space Complexity is O(n^2)
